What is the solution to the compound inequality in interval notation? 2(x+3)>6 or 2x+3≤−7 (−∞, 0) or [5, ∞) (−∞, −5] or (2, ∞) (−∞, −2] or (0, ∞) (−∞, −5] or (0, ∞)

Question

asked Jul 8, 2018 232k views

2 Answers

Tomasantunes · Answer 1 · 2018-07-11T16:11:06+0000

Answer: The correct option is

(D) (−∞, −5] or (0, ∞).

Step-by-step explanation: We are given to select the solution to the following inequality in interval notation :

$2(x+3)>6~~\textup{or}~~2x+3\leq-7~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)$

To find the correct solution, we need to solve both the inequalities in (i) separately.

The solution of (i) is as follows :

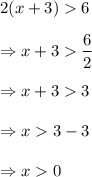
$2(x+3)>6\\\\\Rightarrow x+3>(6)/(2)\\\\\Rightarrow x+3>3\\\\\Rightarrow x>3-3\\\\\Rightarrow x>0$

and

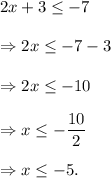
$2x+3\leq -7\\\\\Rightarrow 2x\leq-7-3\\\\\Rightarrow 2x\leq-10\\\\\Rightarrow x\leq-(10)/(2)\\\\\Rightarrow x\leq -5.$

That is, the solution is given by

$x\epsilon (-\infty,-5]~or~(0,\infty).$

Thus, (D) is the correct option.