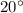Answer:
The values of
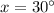 and
and
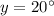 .
.
Explanation:
A Linear pair is a pair of adjacent angles formed when two lines intersect.
In the given figure,
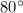 and
and
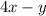 ,
,
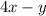 and
and
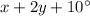 form a linear pair.
form a linear pair.
By linear pairs theorem, we have

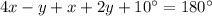
On solving we get,
 ....(1)
....(1)
 .....(2)
.....(2)
Now, to solve equation (1) and (2) by simultaneously; we get
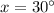
putting the value of x in equation 1 we get,

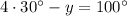
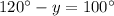
On simplify we have,
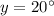
Therefore, the values of x and y are:
 and
and