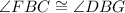Question

FBC and CBG are supplements, DBG and DBF are supplements, and CBG DBF. By the congruent supplements theorem, what can you conclude?

Answer 1

B. ∠FBC ≅ ∠DBG

Answer 2

We will use Congruent supplements theorem, which states If 2 angles are supplementary to the same angle, then they are congruent to each other.

Since, angles FBC and CBG are supplements to each other.

So,
`\angle FBC \cong \angle CBG`

Angles DBG and DBF are supplements to each other.

So,
`\angle DBG \cong \angle DBF`

And angles CBG and DBF are supplements to each other.

So,
`\angle CBG \cong \angle DBF`

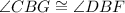
By using these congruent conditions, we conclude that angles FBC and DBG are congruent to each other.

Therefore,
`\angle FBC \cong \angle DBG`