Question

Which point is a solution to the following Inequality3x - y > 4

Answer 1

We have to find a point that is a solution to the following inequality:

`3x-y>4`

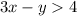
We can rearrange this to assign a value to x and then find a value of y that makes the point be a solution.

We can rearrange it as:

`\begin{gathered} 3x-y>4 \\ 3x>4+y \\ 3x-4>y \\ y<3x-4 \end{gathered}`

Then, we can assign a value to x, like x = 0, and find the range of values that satisfy the inequality when x = 0:

`\begin{gathered} y<3(0)-4 \\ y<-4 \end{gathered}`

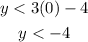
This means that if x = 0, then y has to be less than -4. Then, for example, (0,-6) is a solution to the inequality.

We can see it in a graph as:

The red shaded region is the solution region. Any point in this regions is a solution to the inequality. The dashed line is the line 3x-y = 4.

We can also check with the values of x and y in the inequality:

`\begin{gathered} 3(0)-(-6)>4 \\ 0+6>4 \\ 6>4\longrightarrow\text{True} \end{gathered}`

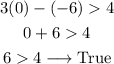
As it is true, we know that the point is part of the solution region.

Answer: one solution to the inequality is (0,-6).