Question

Algebra 1 slope intercept form: write an equation

Answer 1

Ok, so

A line passes through the points (20,-14) and (4,-14). We are asked to find the equation of this line.

First, we're going to find the slope of the line.

For this, remember that:

Given two points (x1,y1) and (x2,y2), the slope (m) between them can be found using the equation:

`m=(y_2-y_1)/(x_2-x_1)_{}`

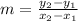
If we replace our values, we notice that:

`\begin{gathered} x_1=20 \\ x_2=4 \\ y_1=-14 \\ y_2=-14 \end{gathered}`

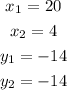
And replacing in the equation:

`m=(-14-(-14))/(4-20)=(0)/(-16)=0`

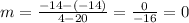
The slope of our line is 0.

Now, given the slope "m" and one point (x1,y1), the equation in slope-intercept form can be found using the formula:

`y=y_1+m(x-x_1)`

Replacing (x1,y1) as (4,-14) and m=0:

`\begin{gathered} y=-14+0(x-4) \\ y=-14 \end{gathered}`

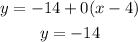
Therefore, the equation of the line is y=-14