Question

Find (d^2)y/d(x^2) in terms of x and y of (x^2)(y^2) - 6 x = 6

using implicit differentiation


(2(x^2)(y^4)-3x(y^2)-3)/((x^4)(y^3) is not the right answer and i'm not sure y.

Answer 1

implicit differentiation one time

then solve for dy/dx
then take derivitive again
I will explain later


first time
dy/dx

`2xy^2+2yx^2 \space\ (dy)/(dx)-6=0`
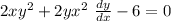
solve for
`(dy)/(dx)`
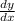
add 6 to both sides and minus 2xy²

`2yx^2 \space\ (dy)/(dx)=6-2xy^2`
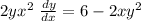
divide both sides by 2yx²

`(dy)/(dx)=(6-2xy^2)/(2yx^2)`

`(dy)/(dx)=(3-xy^2)/(xy^2)`

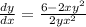
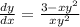
now we do it again
but this time, if you take the derivitive of y, we replace it with dy/dx or
`(3-xy^2)/(xy^2)`

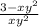
use quotient rule


`(dy^2)/(dx^2)=((-2xy^3 \space\ (dy)/(dx))(xy^2)-(2xy^3 \space\ (dy)/(dx))(3-xy^2))/(x^2y^6)`

`(dy^2)/(dx^2)=((-2xy^3)((3-xy^2)/(xy^2))(xy^2)-(2xy^3)((3-xy^2)/(xy^2))(3-xy^2))/(x^2y^6)`

`(dy^2)/(dx^2)=((-2xy^3)(3-xy^2)-(2xy^3)((3-xy^2)/(xy^2))(3-xy^2))/(x^2y^6)`

`(dy^2)/(dx^2)=((-6xy^2+2x^2y^5)-((6xy^2-2x^2y^5)/(xy^2))(3-xy^2))/(x^2y^6)`

`(dy^2)/(dx^2)=((-6xy^2+2x^2y^5)-((18xy^2-6x^2y^5-6x^2y^4+2x^3y^7)/(xy^2)))/(x^2y^6)`
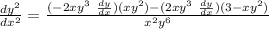
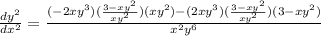
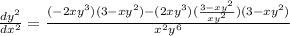
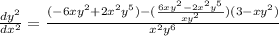
just simplify because I don't have my calculator right now