Question

Find the equilibrium quantity and equilibrium price for the commodity whose supply and demand functions are given.

​Supply: p equals q squared plus 20 qp=q2+20q    ​Demand: p equals negative 4 q squared plus 10 q plus 18 comma 600p=−4q2+10q+18,600

The equilibrium quantity is q= ?

Answer 1

Rewriting the two equations:

[Supply]
`p = q^2+20`
[Demand]
`p=-4q^2+10q+18600`

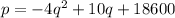
Equilibrium price is when
Supply = Demand

`q^2+20 = -4q^2+10q+18600`

`q^2+4q^2+20-10q-18600 = 0`

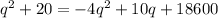
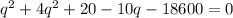
`5q^2-10q-18580=0` ⇒ Simplifying the equation by dividing each term by 5


`q^2-2q-3716=0`

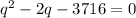
The simplified equation is in quadratic form.
There are three main methods for solving a quadratic equation: factorizing, completing the square, or quadratic formula.

Using the formula, we need the value of a, b, and c which is the constant of the quadratic equation.

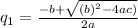
`q_1= (-b+ √((b)^2-4ac)) )/(2a)`, and
`q_2= (-b- √((b)^2-4ac)) )/(2a)`


We have a = 1, b = -2, and c = -3716
Substituting these values into the formula we have

`q_1= (-(-2)+ √((-2)^2-4(1*-3716)) )/(2) =61.97`

`q_2= (-(-2)- √((-2)^2-4(1*-3716)) )/(2) =-59.97`

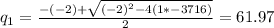
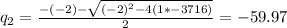
Since 'q' represents a quantity, we can't have negative values, so we choose the value of 'q' to be 61.97 ≈ 62 (rounded to the nearest whole number)

Answer: Equilibrium quantity = 62