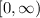Question

Hello, I am having such a hard time solving for restrictions of functions. Could you please show me the steps to solving number 13?

Answer 1

Lets gfind the composite function first:

`\begin{gathered} s(q(x))=s(5√(x)) \\ =(1)/(5)(5√(x))^2 \\ =(25x)/(5) \\ =5x \end{gathered}`

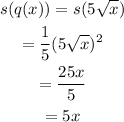
Therefoe , we have:

`s(q(x))=5x`

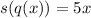
Now, to find the domain we need to remember that the domain of the function s(q(x)) is the set of numbers x in the domain of q for which q(x) is in the domain of s. To find it we will make the following steps:

• Find the doain of sq.

,

• Find the domain of s.

,

• Find the values x in the domain of q for which q(x) is in the domain of f; that is, we will exclude the values, x, form the domain of q for which q(x) is not in the domain of f.

We know that the functio q is tdefinesd as:

`q(x)=5√(x)`

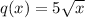
and we know that, in the real numbers, the square root for negative numbers is not defied which means that x has to be a non-*egative number in order for sqto be defined, tahat is:

`dom\text{ }q=\lbrack0,\infty)`

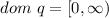
Now, function s is defined as:

`s(x)=(1)/(5)x^2`

and since this is a polynomial, its domain is all the real number set, that is, the x value for function s can be any number. Then w, don't need to exclude any value of x for function s.

Therefore, the domain of the composite function s(q(x)) is:

`\lbrack0,\infty)`