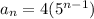Question

The sequences below are either arithmetic sequences or geometric sequences. For each sequence, determine whether it is arithmeticthor geometric, and write the formula for the n term a,, of that sequence.Sequence(a) 11, 16, 21, ...(b) 4, 20, 100,...TypeArithmeticGeometricArithmeticO Geometricthn term formula9,= 09,= 00+0X82 08ロ・ロ

Answer 1

a) Sequence: 11, 16, 21, ...

In this case, the sequence is arithmetic, because it has a defined pattern as a common difference, in specific we have each number separated by +5.

To obtain the formula of an arithmetic sequence we have the equation:

`a_n=a_1+(n-1)d`

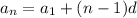
Where d is a common difference.

So if we reply with the numbers we have:

`a_n=11+(n-1)5=5n+6`

Then the correct answer is:

Arithmetic sequence with the formula:

`a_n=5n+6`

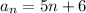
b) sequence: 20, 40, 100, ...

In this case, the sequence is geometric because we have a common factor that determines the sequence, in specific this common factor is x5.

To obtain the formula of an arithmetic sequence we have the equation:

`a_n=a_1(r^(n-1))`

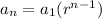
Where r represents the common factor of the sequence.

Then we reply:

`a_n=4(5^(n-1))`

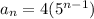
Then the correct answer is:

Geometric sequence with the formula:

`a_n=4(5^(n-1))`