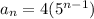a) Sequence: 11, 16, 21, ...
In this case, the sequence is arithmetic, because it has a defined pattern as a common difference, in specific we have each number separated by +5.
To obtain the formula of an arithmetic sequence we have the equation:
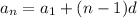
Where d is a common difference.
So if we reply with the numbers we have:

Then the correct answer is:
Arithmetic sequence with the formula:
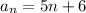
b) sequence: 20, 40, 100, ...
In this case, the sequence is geometric because we have a common factor that determines the sequence, in specific this common factor is x5.
To obtain the formula of an arithmetic sequence we have the equation:
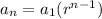
Where r represents the common factor of the sequence.
Then we reply:
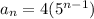
Then the correct answer is:
Geometric sequence with the formula: