Question

Given that x is an integer, Kelvin conjectured that x^2>x+1 .

Which value is a counterexample to Kelvin's conjecture?

−5

0

12

7

Answer 1

The correct anwser is 0

Explanation:

took the test

Answer 2

We calculate the expressions
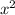
`x^(2)` and
`x+1`

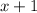
for each of -5, 0, 12 and 7 to see whether the inequality holds:



for x=-5,
`x^(2)=(-5)^2=25`

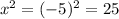
for x=-5
`x+1=-5+1=-4`

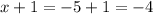
the inequality holds,




for x=0,
`x^(2)=(0)^2=0`

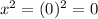
for x=0
`0+1=1`

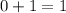
1 is not larger that 0, so x=0 is an counterexample that

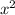
`x^2` is not larger than
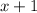
`x+1` for all integers.


Answer: 0