Question

Describe the following variation: y/x2=5

Answer 1

We are asked to describe the variation
`\displaystyle{ (y)/(x^2)=5`,

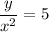
that is
`y=5x^2`

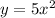
for x≠0, in which case x=y=0, we distinguish the following intervals:

I = (-infinity, -1]
II = (-1, 0)
III = (0, 1)
III = [1, infinity)

Case I, consider the cases (examples) x= -5, and x= -6


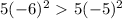
`5(-6)^2\ \textgreater \ 5(-5)^2`, so we can conclude that the greater the x, the smaller the y.

Case II, consider x= -1/2 < x=-1/3


`5(-(1)/(2))^2= (5)/(4)\\\\ 5(-(1)/(3))^2= (5)/(9)\\\\(5)/(9)\ \textless \ (5)/(4)`

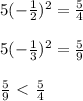thus, the greater the x, the smaller the y.


Case III, consider the cases (examples) x= 5, and x= 6


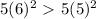
`5(6)^2\ \textgreater \ 5(5)^2`, so we can conclude that the greater the x, the greater the y.

Case III, consider x= 1/3 < x=1/2


`5((1)/(2))^2= (5)/(4)\\\\ 5((1)/(3))^2= (5)/(9)\\\\(5)/(9)\ \textless \ (5)/(4)`

thus, the greater the x, the greater the y.


Conclusion:

y=0 only if x is 0. Otherwise y>0 always:

for x<0, x and y are inversely proportional

for x>0, x and y are directly proportional.


Remark, an other possible consideration in cases could be x<0 and x>0 only.


Remark, another approach is considering the graph of y=5x^2, which is a parabola, with the vertex at (0, 0) opening upwards.

From the graph we can find the same conclusion. That is we can see that the farer we get away from the y-axis, in both direction, the larger the values of y become.