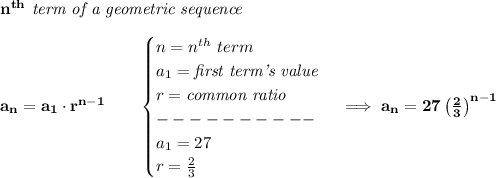Question

Help, I'm bad at math!

A bouncing ball reaches a height of 27 feet at its first peak, 18 feet at its second peak, and 12 feet at its third peak. Describe how a sequence can be used to determine the height of the ball when it reaches its fourth peak.

Answer 1

a bouncing ball issue reaches its next peak as some fraction or multiple of the previous peak, so, that'd make it a geometric sequence.

so, let's take a peek, 27, 18, 12

now, to get the common factor from a geometric sequence, since it's just a multiplier, if you divide any of the terms by the term before it, the quotient is then the common factor, let's do so with hmm say 12 and 18, 12/18 = 2/3 <---- the common factor, you can check if you so wish with 18/27.

and the first term is of course, 27.


`\bf n^(th)\textit{ term of a geometric sequence}\\\\ a_n=a_1\cdot r^(n-1)\qquad \begin{cases} n=n^(th)\ term\\ a_1=\textit{first term's value}\\ r=\textit{common ratio}\\ ----------\\ a_1=27\\ r=(2)/(3) \end{cases}\implies a_n=27\left( (2)/(3) \right)^(n-1)`