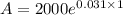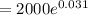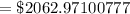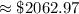Question

Use the formula for continuous compounding to compute the balance in the account after​ 1, 5, and 20 years.​ Also, find the APY for the account. A ​$2000 deposit in an account with an APR of 3.1​%. The balance in the account after 1 year is approximately ____?

Answer 1

`\bf \qquad \textit{Continuously Compounding Interest Earned Amount}\\\\ A=Pe^(rt)\qquad \begin{cases} A=\textit{accumulated amount}\\ P=\textit{original amount deposited}\to& \$2000\\ r=rate\to 3.1\%\to (3.1)/(100)\to &0.031\\ t=years\to &1,5,20 \end{cases} \\\\\\ \stackrel{\textit{for 1 year}}{A=2000e^(0.031\cdot 1)}\qquad \stackrel{\textit{for 5 years}}{A=2000e^(0.031\cdot 5)}\qquad \stackrel{\textit{for 20 years}}{A=2000e^(0.031\cdot 20)}\\\\ -------------------------------\\\\`


`\bf \qquad \qquad \textit{Annual Yield Formula} \\\\ ~~~~~~~~~\left(1+(r)/(n)\right)^(n)-1 \\\\ \begin{cases} r=rate\to 3.1\%\to (3.1)/(100)\to &0.031\\ n= \begin{array}{llll} \textit{times it compounds per year}\\ \textit{continuously, 365 days then} \end{array}\to &365 \end{cases} \\\\\\ \left(1+(0.031)/(365)\right)^(365)-1 \approx 0.03148414 \\\\\\ 0.03148414\cdot 100\implies 3.148\% \approx 3.15\%`

Answer 2

$ 2062.97 ( approx )

Explanation:

Since, the amount formula for continuous compounding,

`A=Pe^(rt)`

Where, P is the principal amount,

r is the rate per period,

t is the number of years,

e is euclid number,

Here,

P = $ 2000,

r = 3.1% = 0.031,

t = 1 year,

Hence, the balance would be,

`A=2000 e^(0.031* 1)`

`= 2000 e^(0.031)`

`=\$ 2062.97100777`

`\approx \$ 2062.97`