Question

Find the x-intercepts and the vertex of the parabola y = (x − 4)(x + 2)Write as ordered pairsWrite the equation y =(x − 4)(x +2)in standard formuse the quadratic formula to identify the x-value of the vertex.Part IV: Substitute the x-value of the vertex from Part III into the original equation to find the y-value of the vertex. Then, write the coordinates of the vertex.

Answer 1

Explanation:

we have:

Part 1) Find the x-intercepts of the parabola and write them as ordered pairs

The x-intercepts are the values of x when the value of y is equal to zero

so

For y=0

`(x-4)(x+2)`

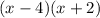
For x=4 and x=-2 the equation is equal to zero

therefore

The x-intercepts are the points (-2,0) and (4,0)

Part 2) Write the equation y=(x-4)(x+2) in standard form

The quadratic equation in standard form is equal to

`y=ax^2+bx+c`

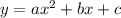
applying distributive property

`\begin{gathered} y=(x-4)(x+2) \\ y=x^2+2x-4x-8 \\ y=x^2-2x-8 \end{gathered}`

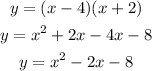
where a = 1, b = -2, c = -8

Part 3) With the standard form of the equation from part ll, use the quadratic formula to identify the x-value of the vertex

we know that

the x-value of the vertex is -b/2a

we have

where a = 1, b = -2, c = -8

substitute

x = -b/2a = -2/2(1) = 1

therefore

The x-coordinate of the vertex is 1

Part 4) Substitute the x-value of the vertex from part lll into the original equation to find the y-value of the vertex.

we have

`y=(x-4)(x+2)`

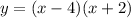
For x=1

substitute and solve for y

`\begin{gathered} y=(1-4)(1+2) \\ y=-3(3) \\ y=-9 \end{gathered}`

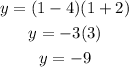
therefore

The y-coordinate of the vertex is -9

The coordinate of the vertex is the point (1,-9)