Let's take a closer look at our vector:
Now, notice that the angle a and the 130° angle given in the plot are a linear pair. This way,
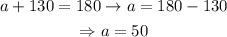
Therefore, our graph would be:
Since this is a right triangle, we'll have that:
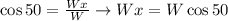
And that:
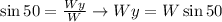
Notice that the horizontal component is going to the left (negative) and that the vertical component is going down (negative). This way, we'll have that:
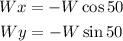
Plugging in the magnitude of the vector (19),
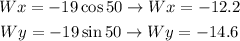
This way, we can conclude that the horizontal component is -12.2 and that the vertical component is -14.6