Question

TRIGONOMETRY Find the horizontal and vertical components of this vector round to the nearest tenth

Answer 1

Let's take a closer look at our vector:

Now, notice that the angle a and the 130° angle given in the plot are a linear pair. This way,

`\begin{gathered} a+130=180\rightarrow a=180-130 \\ \Rightarrow a=50 \end{gathered}`

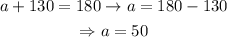
Therefore, our graph would be:

Since this is a right triangle, we'll have that:

`\cos 50=\frac{Wx_{}}{W}\rightarrow Wx=W\cos 50`

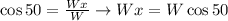
And that:

`\sin 50=(Wy)/(W)\rightarrow Wy=W\sin 50`

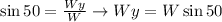
Notice that the horizontal component is going to the left (negative) and that the vertical component is going down (negative). This way, we'll have that:

`\begin{gathered} Wx=-W\cos 50 \\ Wy=-W\sin 50 \end{gathered}`

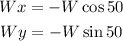
Plugging in the magnitude of the vector (19),

`\begin{gathered} Wx=-19\cos 50\rightarrow Wx=-12.2 \\ Wy=-19\sin 50\rightarrow Wy=-14.6 \end{gathered}`

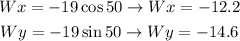
This way, we can conclude that the horizontal component is -12.2 and that the vertical component is -14.6