Question

X is a normally distributed random variable with mean 71 and standard deviation 9.

What is the probability that X is between 60 and 82?
Write your answer as a decimal rounded to the nearest thousandth.

Answer 1

Since the standard deviation is 10 and the first given score is 40, the 40 is 2 standard deviations below the mean.

On the other hand, 80 is 2 standard deviations above the mean.

Thus, we subtract the probability below the z-score which is 2, 0.97725, and the probability below the z-score which is -2, 0.02275.

`\begin{gathered} P(X)=0.97725-0.02275 \\ P(X)=0.9545 \end{gathered}`

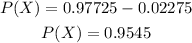
We may obtain the values using the z-score table.

Therefore, the approximate value of the probability is 0.955.