Arc Length
Given a circle of radius r, the length of the arc formed by a central angle θ is given by:
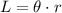
We are given the central angle ∠JKL = 144° and the radius r = JK = 6 units.
The angle must be converted to radians by using the equivalence π = 180°
Thus:
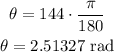
Calculating the arc length:
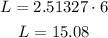
The length of the arc JL is 15.08 units