Answer: 2005
Explanation:
Exponential function to determine the value of item after t years,
 , where r= rate of growth, A=Initial value.
, where r= rate of growth, A=Initial value.
As per given , A = 7.85% = 0.0785
A = $125,000
Substitute all values in function, we get
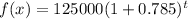
When f(x)= 3A , then
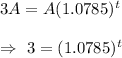
Taking tog on both sides , we get

The year will be 1990+15= 2005
Hence, the required year = 2005