well, for a function, in a set of x,y ordered pairs, so long the "x" are not repeated, then it IS a function, let's look
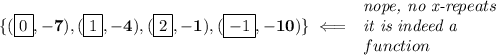
so then, let's use two of those points ahemm let's see say (0, -7) and (2, -1)
so, what's the equation of a
line that goes through (0, -7) and (2, -1)?
![\bf \begin{array}{lllll} &x_1&y_1&x_2&y_2\\ % (a,b) &({{ 0}}\quad ,&{{ -7}})\quad % (c,d) &({{ 2}}\quad ,&{{ -1}}) \end{array} \\\\\\ % slope = m slope = {{ m}}= \cfrac{rise}{run} \implies \cfrac{{{ y_2}}-{{ y_1}}}{{{ x_2}}-{{ x_1}}}\implies \cfrac{-1-(-7)}{2-0}\implies \cfrac{-1+7}{2-0} \\\\\\ \cfrac{6}{2}\implies 3 \\\\\\ % point-slope intercept \stackrel{\textit{point-slope form}}{y-{{ y_1}}={{ m}}(x-{{ x_1}})}\implies y-(-7)=3(x-0)\implies y+7=3x \\\\\\ y=3x-7]()