The probability that a randomly selected student does not enjoy poetry and does not prefer literature is given by
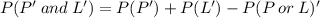
Where P' represents students that do not enjoy poetry and L' represents student do not prefer literature.
Let us first find the probability P(P')
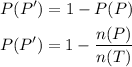
The number of students who enjoy poetry is 20 + 17 = 37
The total number of students in the school is 20 + 17 + 19 + 10 + 16 + 8 = 90
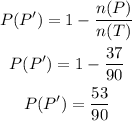
Now, let us first find the probability P(L')
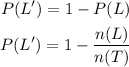
The number of students who prefer literature is 17 + 10 + 8 = 35
The total number of students in the school is 20 + 17 + 19 + 10 + 16 + 8 = 90
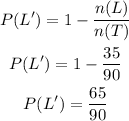
Now, let us first find the probability P(P or L)'
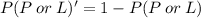
Where
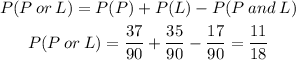
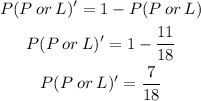
Finally,
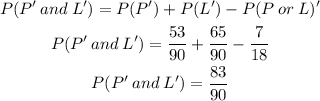
Therefore, the probability that a randomly selected student does not enjoy poetry and does not prefer literature is 83/90