Question

Ms. Lowery surveyed her math students to and school subjects they prefer. Math Literature Poetry 20 17 Student council 19 10 Guitar 16 8 What is the probability that a randomly selected student does not enjoy poetry and does not prefer literature? Simplify any fractions.

Answer 1

The probability that a randomly selected student does not enjoy poetry and does not prefer literature is given by

`P(P^(\prime)\: and\: L^(\prime))=P(P^(\prime))+P(L^(\prime))-P(P\: or\: L)^(\prime)`

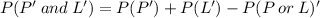
Where P' represents students that do not enjoy poetry and L' represents student do not prefer literature.

Let us first find the probability P(P')

`\begin{gathered} P(P^(\prime))=1-P(P) \\ P(P^(\prime))=1-(n(P))/(n(T)) \end{gathered}`

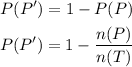
The number of students who enjoy poetry is 20 + 17 = 37

The total number of students in the school is 20 + 17 + 19 + 10 + 16 + 8 = 90

`\begin{gathered} P(P^(\prime))=1-(n(P))/(n(T)) \\ P(P^(\prime))=1-(37)/(90) \\ P(P^(\prime))=(53)/(90) \end{gathered}`

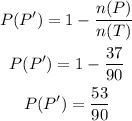
Now, let us first find the probability P(L')

`\begin{gathered} P(L^(\prime))=1-P(L) \\ P(L^(\prime))=1-(n(L))/(n(T)) \end{gathered}`

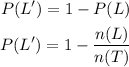
The number of students who prefer literature is 17 + 10 + 8 = 35

The total number of students in the school is 20 + 17 + 19 + 10 + 16 + 8 = 90

`\begin{gathered} P(L^(\prime))=1-(n(L))/(n(T)) \\ P(L^(\prime))=1-(35)/(90) \\ P(L^(\prime))=(65)/(90) \end{gathered}`

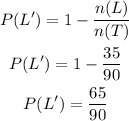
Now, let us first find the probability P(P or L)'

`P(P\: or\: L)^(\prime)=1-P(P\: or\: L)`

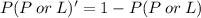
Where

`\begin{gathered} P(P\: or\: L)=P(P)+P(L)-P(P\: and\: L) \\ P(P\: or\: L)=(37)/(90)+(35)/(90)-(17)/(90)=(11)/(18) \end{gathered}`
`\begin{gathered} P(P\: or\: L)^(\prime)=1-P(P\: or\: L) \\ P(P\: or\: L)^(\prime)=1-(11)/(18) \\ P(P\: or\: L)^(\prime)=(7)/(18) \end{gathered}`

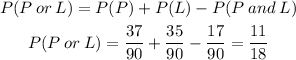
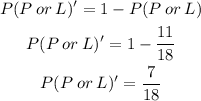
Finally,

`\begin{gathered} P(P^(\prime)\: and\: L^(\prime))=P(P^(\prime))+P(L^(\prime))-P(P\: or\: L)^(\prime) \\ P(P^(\prime)\: and\: L^(\prime))=(53)/(90)+(65)/(90)-(7)/(18) \\ P(P^(\prime)\: and\: L^(\prime))=(83)/(90) \end{gathered}`

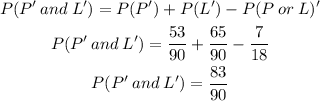
Therefore, the probability that a randomly selected student does not enjoy poetry and does not prefer literature is 83/90