Question

Rework problem 5 from section 2.4 of your text (page 81) about randomly selecting 3 cans of regular and diet cola, but assume that there are 6 cans of regular cola and 8 cans of diet cola.

What is the probability that 2 cans of regular cola and 1 can of diet cola are selected?

Answer 1

The formula
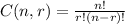`C(n, r)= (n!)/(r!(n-r)!)`, where r! is 1*2*3*...r

is the formula which gives us the total number of ways of forming groups of r objects, out of n objects.

for example, given 10 objects, there are C(10,6) ways of forming groups of 6, out of the 10 objects.

---------------------------------------------------------------------------------------------------

There are 6 cans of regular cola, and 8 cans of diet cola.

in short, let's use the letters R, for regular, and D for diet cola.

So we have 6 R and 8 D. 14 in total.


There are C(14, 3) many ways of picking 3 cans out of 14, so there are


`\displaystyle{ C(14, 3)= (14!)/(3!\cdot11!)= (14\cdot13\cdot12)/(3\cdot2)=14\cdot13\cdot2= 364`

ways of forming groups of 3 cans.



Consider the event "2 cans of regular cola and 1 can of diet cola are selected",

this may happen in C(6, 2)*C(8, 1) many ways, since there are C(6, 2) ways of selecting 2 regular colas out of 6, which can be combined with C(8, 1) ways of selecting 1 diet cola out of 8.


`C(6, 2)\cdot C(8, 1)=\displaystyle{ (6!)/(2!4!)\cdot (8!)/(1!7!)= (6\cdot5\cdot4!)/(2!4!)\cdot8=15\cdot8= 120`



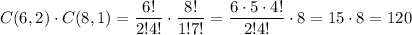
P(2 cans of regular cola and 1 can of diet cola)=120/364=0.33


Answer: 0.33