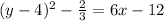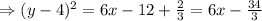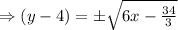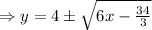Question

Which equation is the inverse of (x-4)^2-2/3=6y-12

Answer 1

`The \ inverse \ of \ (x-4)^(2)-(2)/(3) =6y-12 \ is \ y= 4\pm \sqrt{6x-(34)/(3)}`

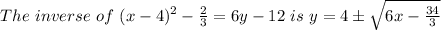
Solution-

The given function,

`(x-4)^(2)-(2)/(3) =6y-12`

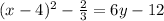
The inverse of a function normally means switching the role of the variables. ( y becomes the input or independent variable, and x becomes the output or the dependent variable)

Switching x and y, the function becomes,

`(y-4)^(2)-(2)/(3) =6x-12`

`\Rightarrow (y-4)^(2)= 6x-12 +(2)/(3)=6x-(34)/(3)`

`\Rightarrow (y-4)= \pm \sqrt{6x-(34)/(3)}`

`\Rightarrow y= 4\pm \sqrt{6x-(34)/(3)}`