Consider the given equation,
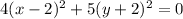
Divide the equation by 20 i.e. LCM of 5 and 4,
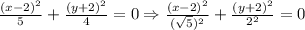
The equation does not resemble an ellipse or circle.
Either it is a point, or none of the above.
Let us check if the equation resembles a point.
Consider the equation as,
![5(y+2)^2=-4(x-2)^2\Rightarrow(y+2)^2=-(4)/(5)(x-2)^2\Rightarrow y+2=\sqrt[]{-(4)/(5)(x-2)^2}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/bxcujssqz7ayk203n5xu.png)
Simplify the expression further,
![y+2=(x-2).\sqrt[]{(-4)/(5)}\Rightarrow y=2+(x-2).\sqrt[]{(-4)/(5)}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/4srp48ahgrn6fcawbqbi.png)
Now, observe that for every value of 'x' there exist some value of 'y'. It means that the equation corresponds to a point.
But note that there is a negative term in the square root i.e. imaginary term.
It means that this point must lie in a complex plane, not on the real plane.
Therefore, the answer to the given question is a point.nary