Question

Sophie earned a score of 216 on Exam A that had a mean of 200 and a standarddeviation of 20. She is about to take Exam B that has a mean of 450 and a standarddeviation of 40. How well must Sophie score on Exam B in order to do equivalentlywell as she did on Exam A? Assume that scores on each exam are normallydistributed

Answer 1

Concept

Apply z scores

First, let's find the z-score that corresponds to the information given for Exam A.

`\begin{gathered} \text{Mean }\mu\text{ = 200} \\ \text{Standard debiation }\sigma\text{ = 20} \\ z\text{ = }\frac{x\text{ - }\mu}{\sigma} \\ \text{Substitute the following values} \\ x\text{ = 2}16 \\ \sigma\text{ = 20} \\ \mu\text{ = 200} \\ z\text{ = }\frac{216\text{ - 200}}{20} \\ z\text{ = }(16)/(20) \\ z\text{ = 0.8} \end{gathered}`

For Sophie to do equivalently well in Exam B as well as she did on Exam A, we find the value of x by using the z score of exam A.

The formula for finding a z-score is shown below:

`\begin{gathered} \text{Exam B} \\ x\text{ = ?} \\ z\text{ score = 0.8} \\ \mu\text{ = 450} \\ \sigma\text{ = 40} \end{gathered}`

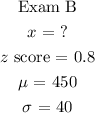
Next, substitute the following values to find the value of x.

`\begin{gathered} \text{Therefore,} \\ z\text{ = }\frac{x-\text{ }\mu}{\sigma} \\ 0.8\text{ = }\frac{x\text{ - 450}}{40} \\ \text{Cross multiply} \\ x\text{ - 450 = 0.8 x 40} \\ x\text{ - 450 = 32} \\ \text{x = 450 + 32} \\ x\text{ = 482} \end{gathered}`

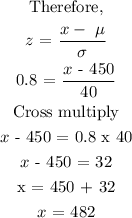
Final answer

x = 482