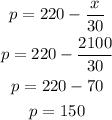Solution:
Given:
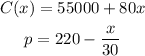
To get the production level that will lead to maximum profit, we need to get the revenue.
Revenue (R) is price multiplied by the number of electric drills.
Hence,
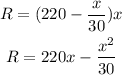
Part A:
Profit is the difference between revenue and cost;
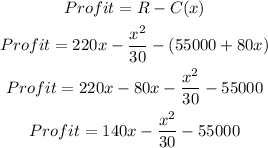
Therefore,
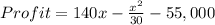
To get the production level, we find the maximum value from the profit.
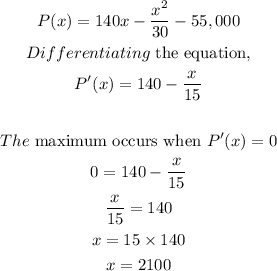
Therefore, the production level that results in maximum profit is 2100.
Part B:
The price to maximize profit is;