Question

A student bikes to school by traveling first dN = 1.00 miles north, then dW = 0.600 miles west, and finally dS = 0.200 miles south. T ake the north direction as the positive 

y  direction and east as positive  x . The origin is still where the student starts biking. Let  d⃗  N  be the displacement vector corresponding to the first leg of the student's trip. Express  d⃗  N  in component form

Answer 1

Refer to the diagram shown below.

Define unit vectors along the x and y axes as respectively
`\hat{i} \, and \, \hat{j}.`

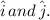
Then the three successive displacements, written in component form, are respectively

`\vec{dN} = 1.0 \, \hat{j} \\ \vec{dW} = -0.6 \, \hat{i} \\ \vec{dS} = -0.2 \, \hat{j}`

The total displacement for the first leg of the trip is

`\vec{d} = \vec{dN} + \vec{dW} + \vec{dS} \\ \vec{d}= 1.0\hat{j}-0.6\hat{i}-0.2\hat{j} \\ \vec{d}=-0.6\hat{i}+0.8\hat{j}`

Answer:

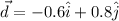
`\vec{d} = -0.6\hat{i}+0.8\hat{j}` or (-0.6, 0.8)