Question

Hard math question!

What is the inverse matrix of
`\left[\begin{array}{cc}a&b\\c&d\end{array}\right]`?
Please show work!

Answer 1

First, let me show you some notation.

To show a matrix is an inverse of another matrix, we write
`A^(-1)`

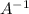
-1 is not an exponent. It just shows that a matrix is an inverse of another matrix.

For a 2x2 matrix, we can get the inverse by first making b and c negatives and swap the positions of a and d.

Then multiply each entry in the matrix by 1 divided by the determinant.


`\left[\begin{array}{ccc}a&b\\c&d\end{array}\right]^(-1) = (1)/(ad - bc)\left[\begin{array}{ccc}d&{-b}\\{-c}&a\end{array}\right] = \\ \\ \\ \left[\begin{array}{ccc}d((1)/(ad-bc))&{-b}((1)/(ad-bc)) \\ {-c}((1)/(ad-bc)) &a((1)/(ad-bc)) \end{array}\right]`

I hope this helped!