Question

Consider this scenario: A traffic signal for eastbound traffic is red for 15 seconds, yellow for 5 seconds, and green for 30 seconds. The traffic policemen want to know the probability that out of the next x number of eastbound cars that arrive at that signal(where x>3), 3 of them would be stopped by a red light. What is the probability that out of the next 8 eastbound cars that arrive at the signal, exactly 3 will be stopped by a red light? 0.254 0.552 0.806 0.448

Answer 1

P(3 reds out of 8)
= 8C3 * [15 / (15 + 5 + 30)]^3 * [(5 + 30) / (15 + 5 + 30)]^(8 - 3)
= 8C3 * 0.3^3 * 0.7^5
= 0.25412184
= 25.4%
=~ 0.3

Answer 2

0.254

Explanation:

Given : A traffic signal for eastbound traffic is red for 15 seconds, yellow for 5 seconds, and green for 30 seconds.

To Find: What is the probability that out of the next 8 eastbound cars that arrive at the signal, exactly 3 will be stopped by a red light?

Solution:

A traffic signal for eastbound traffic is red for 15 seconds, yellow for 5 seconds, and green for 30 seconds.

Total time = 15+5+30=50

So, probability of occurring red light =
`(15)/(50)=0.3`

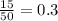
So, Probability of not occurring red light =
`1-0.3=0.7`

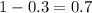
Now we are supposed to find the probability that out of the next 8 eastbound cars that arrive at the signal, exactly 3 will be stopped by a red light

So, we will use binomial

`P(X=r)=^nC_r p^rq^(n-r)`

Substitute n = 8

r = 3

p is the probability of success that is probability of occurring red light = 0.3

q is the probability of failure that is probability of not occurring red light=0.7

So,
`P(X=3)=^(8)C_(3) (0.3)^3 (0.7)^(5)`

`P(X=3)=(8!)/(3!(8-3)!)(0.3)^3 (0.7)^(5)`

`P(X=3)=0.254`

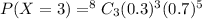
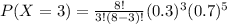
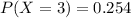
Thus the probability that out of the next 8 eastbound cars that arrive at the signal, exactly 3 will be stopped by a red light is 0.254

Hence Option A is true.