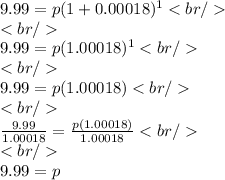Question

If the interest rate on a savings account is 0.018%, approximately how much money do you need to keep in this account for 1 year to earn enough interest to cover a single $9.99 Below-Minimum-Balance Fee?

Answer 1

The correct answer is:

$9.99

Step-by-step explanation:

The formula for compound interest is

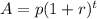`A=p(1+r)^t`, where A is the total amount, p is the principal invested, r is the interest rate as a decimal number, and t is the number of years. In our problem, A is 9.99 (enough to cover the fee); p is unknown; r is 0.018% = 0.018/100 = 0.00018; and t is 1:

`image`

Answer 2

We are not told how often the interest is compounded, so assuming it is compounded yearly, you need to keep $9.99 in the account to pay the fee.

Explanation:
Compound interest follows the formula A=p(1+r)^t,
where:
A is the total amount in the account,
p is the amount of principal,
r is the interest rate as a decimal number,
and t is the number of years.

For our problem:
A = 9.99,
p is unknown,
r = 0.018% = 0.00018,
and t=1.

This gives us:
9.99=p(1+0.00018)^1;
9.99=p(1.00018).

Divide both sides by 1.00018:
9.99=p.