Answer:
The correct option is C.) AB = 5
Explanation:
the diagram of given triangle is shown in figure-1
M, N and O correspond to A , B and C respectively.
and also given that triangle MNO is 0.5 times of triangle ABC
so, MN =(0.5)AB , NO = (0.5)BC and MO =(0.5)AC
then
MO =(0.5)AC
Put OM = 5
5 =(0.5)AC
Divide both the sides by 0.5,
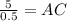
10 = AC
If AB = x and AC = 2x
AC = 2x
10 = 2x
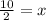
5 = x
since AB = x the AB = 5
hence, correct option is C.) AB = 5