Question

A brick is thrown upward from the top of a building at an angle of 35° to the horizontal and with an initial speed of 14 m/s. If the brick is in flight for 3.1 s, how tall is the building?_____ m

Answer 1

Given:

The angle made by brick with horizontal is: θ = 35°.

The initial speed of the brick is: Vi = 14 m/s.

The brick is in flight for the time of: t = 3.1 s.

To find:

The height of the building.

Step-by-step explanation:

To determine the height of the building, we need to calculate the vertical displacement of the brick.

The initial vertical velocity Viy of the brick, when thrown upwards with velocity Vi, can be calculated as:

`V_(iy)=V_isin\theta`

Substituting the values in the above equation, we get:

`\begin{gathered} V_(iy)=14* sin35\degree\text{ m/s} \\ \\ V_(iy)=8.03\text{ m/s} \end{gathered}`

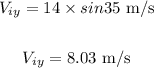
As the brick is thrown in an upwards direction against gravity, the acceleration "ay" will be - 9.8 m/s².

`a_y=-9.8\text{ m/s}^2`

Now, the height "H" of the building can be calculated as:

`-H=V_(iy)t+(1)/(2)a_yt^2`

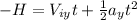
The negative sign of the height "H" indicates that the height is measured in the opposite direction from the top to the bottom of the building.

Substituting the values in the above equation, we get:

`\begin{gathered} -H=8.03\text{ m/s}*3.1\text{ s}-(1)/(2)*9.8\text{ m/s}^2*\text{ \lparen}3.1\text{ s\rparen}^2 \\ \\ -H=24.90\text{ m}-47.09\text{ m} \\ \\ -H=-22.19\text{ m} \\ \\ H\approx22.20\text{ m} \end{gathered}`

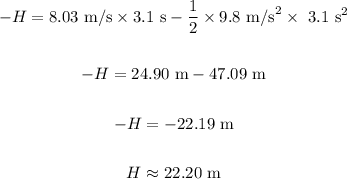
Final answer:

The building is 22.20 m tall.