Answer:
C.

Explanation:
We have been given a pair of points on a graph of an inverse variation. We are asked to find the missing value for our given point.
We know that when y varies inversely with x, then the equation is:
 , where, k represents constant of variation.
, where, k represents constant of variation.
First of all, we will find constant of variation using point
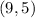 as shown below:
as shown below:
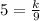

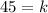
Upon substituting
 in inversely proportion we will get:
in inversely proportion we will get:
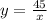
To find the value of x, we will substitute
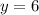 in our equation as:
in our equation as:

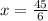
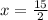

Therefore, the missing value is
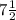 and option C is the correct choice.
and option C is the correct choice.