Question

Solve 3x^2-y^2)dx+(xy-x^3y^{-1})dy=0 through homogenous equations

I've gotten to y(y^2-3x^2)/x(y^2-x^2) but don't know what to do from there

Answer 1

First you have to make the diff equation exact by multiplying by an integrating factor.

The integrating factor will be in the form:
`x^a y^b`

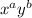
This gives:

`(3x^(a+2)y^b - x^a y^(b+2)) dx+ (x^(a+1) y^(b+1) - x^(a+3) y^(b-1)) dy = 0`

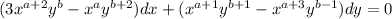
Now set partial derivatives equal to find a,b.


`M dx + N dy = 0 \\ \\ M_y = N_x`


`M_y = 3b x^(a+2) y^(b-1) -(b+2) x^a y^(b+1) \\ \\ N_x = (a+1)x^a y^(b+1) - (a+3)x^(a+2) y^(b-1)`

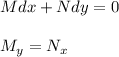
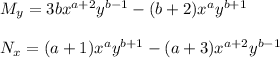
Setting coefficients equal we have:

`a+1 = -(b+2) \\ \\ -(a+3) = 3b`

Solving this system of 2 equations yields:

`a = -3, b = 0`

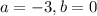
Now you have an exact diff equation:

`(3x^(-1) - x^(-3) y^2 )dx + (x^(-2)y - y^(-1)) dy = 0`

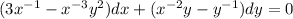
The solution is:

`\int M dx= \int N dy = C`


`\int M dx = \int (3 x^(-1) -x^(-3) y^2) dx = 3 ln (x) + (1)/(2)x^(-2) y^2 + h(y)`


`\int N dy = \int (x^(-2)y - y^(-1) ) dy = (1)/(2)x^(-2) y^2 - ln (y) + h(x)`

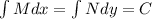
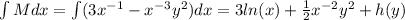
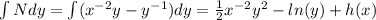
h(y) and h(x) are constants in terms of the specified variable.
By equating the 2 integrals, you can see that

`h(y) = -ln(y) \\ \\ h(x) = 3 ln (x)`

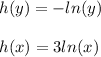
Finally, the general solution is:

`(1)/(2) x^(-2) y^2 + 3ln(x) - ln(y) = C`