Question

Simplify the expression x2 + 1 as much as possible after substituting cot(θ) for x. (Assume 0° < θ < 90°.)

Answer 1

Remark: we are going to use the following identities:

i) cot(x)=cos(x)/sin(x)

ii)
`sin ^(2) x+cos^2 x=1`,

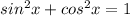
iii) 1/ (sin x) = csc(x)



x^2+1=cot^2(∅)+1=[cos(∅)/sin(∅)]^2+1 by identity i

=[cos^2(∅)]/[sin^2(∅)]+(sin^2∅)/(sin^2∅)

=[cos^2(∅)+sin^2(∅)]/ [sin^2(∅)]=1/ [sin^2(∅)] by identity ii

=[ 1/ sin(∅)]^2=csc^2(∅) by identity iii


Answer: csc^2(∅)