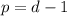Answer:
7.The solution to the set of equation in the form (-5,-3).
8.Multiply equation A by -4 used to eliminate the z- term.
9.Step 2:
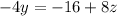 { equation A in step1 is simplified}.
{ equation A in step1 is simplified}.
10.
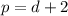
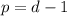 .
.
Explanation:
7. Two equation are given below:
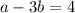
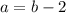
II eqaution can be write as
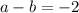
Subtracting equation II from equation I then we get
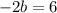
By division property of equality
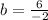
By simplification we get
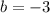
Substitute the value of b in equation I then we get

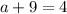
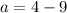
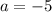
Hence, the solution of the set of equation is (-5,-3).
8. Equation A:
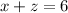
Equation B:
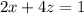
Equation A is multiplied by -4 then we get
Equation A:
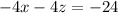
Adding both equation A and B then we get
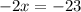
Answer: Multiply equation A by -4 to eliminate the z-term.
9.Equation A:
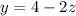
Equation B:
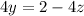
Step1 :
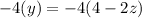
Equation A is multiplied by -4
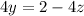 [equation B]
[equation B]
Step 2:
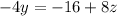
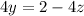 [equation B]
[equation B]
Equation A in step1 s simplified .
Step3:
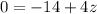
Equations in step 2 are added.
Step 4:
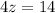
Step5:

Hence, in step 2 student did make first an error.
10. Given
Variable p is more than variable d
We can write in algebraic expression

Variable p is also 1 less than variable d.
Then the algebraic expression
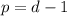
Hence,