We have that the measure of an external angle in a triangle is the sum of the non-adjacent angles to this external angle. Then, we have that:
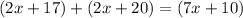
And now, we can solve this equation by summing like terms. Then, we have:
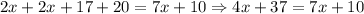
We need to subtract 4x to both sides of the equation:

Now, subtract 10 from both sides of the equation:
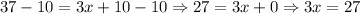
Divide both sides of the equation by 3:
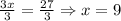
And we have the value for x. However, we need to find the value for m< VWX = (7x+10). We need to plug the value of x in this equation. Then, we have:
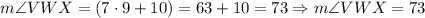
Hence, the value for m