Answer: The required length of the given segment is 13 units.
Step-by-step explanation: We are given to find the length of the segment AB with endpoints A(3, 2) and B(8, 14).
We have the following distance formula :
Distance formula : The length of a line segment with endpoints (a, b) and (c, d) is given by
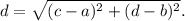
Therefore, the length of the segment AB is given by
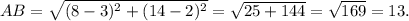
Thus, the required length of the given segment is 13 units.