Answer:
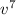 x (6v+7) x (3v+2)
x (6v+7) x (3v+2)
Explanation:
18v^9 + 33v^8 +14v^7
Factor out v^7 from the expression
v^7 x (18v^2+33v+14)
write 33v as a sum
v^7 x (18v^2+21v+12v+14) *like this 21v+12v
Factor out 3v from the expression
v^7 x (3v x (6v+7)+12v+14)
Factor out 2 from the expression
c^7 x (3v x (6v+7)+2(6v+7)
Factor out 6v+7 from the expression
v^7 x (6v+7) x (3v+2)