Question

In physics, it is important to use mathematical approximations. for instance, in a small angle approximation, tanα ∼ sin α . find the largest angle α for which the difference between the sine and the tangent of an angle is less than 10.4% of the sinα value. answer in units of rad.

Answer 1

Note that x is measured in radians.
The percent difference or error between sin(x) and tan(x) is calculated as

`d = 100( (|sin(x)-tan(x)|)/(sin(x)) )`

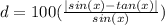
We want this percent difference to be less than 10.4%.
Because tan(x) > sin(x) for small values of x, define

`f(x) = (tan(x)-sin(x))/(sin(x))= 0.104 \\ or \\ sec(x) - 1 = 0.104 \\ sec(x) = 1.104`

From the calculator, obtain
sec⁻¹ 1.104 = 0.4375

Answer: x = 0.4375 radians