Applying the derivative of the trigonometric functions, the derivative of tan x is sec²x.
Hence, the derivative of tan (3x + 3 ) is sec² (3x + 3) times the derivative of 3x - 3 which is 3.
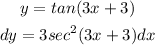
To find the differential dy when x = 5 and dx = 0.4, simply replace the x and dx in the dy function with their given values.
![dy=\lbrace3sec^2[(3(5)+3)]\rbrace(0.4)](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/oqrb54m96phc5o5rbmdq.png)
Then, simplify.
](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/xg6zmijh4mvwphikywkm.png)
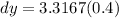
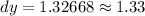
Hence, at x = 5 and dx = 0.4, the differential dy is approximately equal to 1.33.
For x = 5 and dx = 0.8, we do the same process above but this time, multiply the derivative by 0.8.
](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/lq1p44i7lsv9wmisdmjp.png)
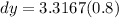
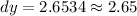
Hence, at x = 5 and dx = 0.8, the differential dy is approximately equal to 2.65.