The perimeter of a polygon is the sum of the lengths of its sides. In this case, since the lengths of the sides of the triangle are a, b and c, then its perimeter is given by:
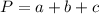
On the other hand, the area of a triangle is given by half the product of its base and its height:
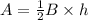
The base of a triangle is one of its sides, and the height is the perpendicular length that joins the vertex opposite to the base with the base.
In this case, since the sides with lengths a and b are perpendicular, we can consider them to be the base and the height of the triangle. Then, the area of the triangle is:
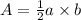
Replace a=7.5cm, b=4.4cm and c=8.7cm to find the perimeter and the area of the given triangle:
![\begin{gathered} P=a+b+c \\ =(7.5\operatorname{cm})+(4.4\operatorname{cm})+(8.7\operatorname{cm}) \\ =20.6\operatorname{cm} \end{gathered}]()
![\begin{gathered} A=(1)/(2)a* b \\ =(1)/(2)(7.5\operatorname{cm})*(4.4\operatorname{cm}) \\ =(1)/(2)\cdot33\operatorname{cm}^2 \\ =16.5\operatorname{cm}^2 \end{gathered}]()
Finally, remember that if one of the internal angles of a triangle is a right angle (such is the case of the image), then the triangle is called a right triangle.
Therefore, the answers are:
Area: 16.5cm²
Perimeter: 20.6cm
Type: Right triangle