Question

The table shows the cost for traveling on a toll road in Henderson. The graph shows the cost of traveling on a toll road in Clarkson. Compare the linear functions to determine which is a direct variation. Justify your response.

Answer 1

A direct variation (also known as proportional) relationship always include the center of coordinates (0,0) in the line. In direct variation relationships, the quotient y/x is constant for any point in the line and this constant is the value of the slope of the line.

In this case, the toll road in Clarkson starts at (0,2), not including the center of coordinates (0,0). Then, it is not a direct variation relationship.

The ratio y/x is not constant:

`\begin{gathered} (4.5)/(10)=0.45 \\ (3.25)/(5)=0.65 \\ (4.5)/(10)\\eq(3.25)/(5) \end{gathered}`

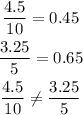
In the case of the toll road in Henderson, the relationship includes the point (0,0) so it is a direct variation relationship.

We can verify that the ratio y/x is constant:

`(y)/(x)=(3)/(10)=(6)/(20)=(9)/(30)=0.3`

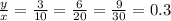
Answer: The toll road in Henderson responds to a direct variation function.