The given function is

The general form of the cosine function is
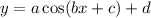
a is the amplitude
2pi/b is the period
c is the phase shift
d is the vertical shift
By comparing the two functions
a = 4
b = pi
c = 0
d = 1
Then its period is
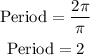
The equation of the midline is

Since the maximum is at the greatest value of cos, which is 1, then

Since the minimum is at the smallest value of cos, which is -1, then

Then substitute them in the equation of the midline
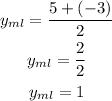
The answers are:
Period = 2
Equation of the midline is y = 1
Maximum = 5
Minimum = -3