Question

A furniture maker uses the specification 21.88 (<=) w (<=)22.12 for the width w in inches of a desk drawer. Write the specification as an absolute value inequality.

A) |w- 0.24|(<=) 22.12
B) |w- 22 |(<=) 0.24
C) |w- 0.12| (<=) 22
D) |w- 22| (<=) 0.12

its not A

Answer 1

Option D is correct

`|w-22|\leq 0.12`

Explanation:

If absolute value inequality is:
`|X-a| \leq b` then;

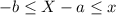`-b\leq X-a\leq x` .....[1]

As per the statement:

A furniture maker uses the specification for the width w in inches of a desk drawer.

`21.88 \leq w \leq 22.12`

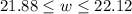
Subtract 22 from each side we get;

`21.88-22 \leq w-22 \leq 22.12-22`

Simplify:

`-0.12 \leq w-22 \leq 0.12`

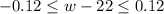
From [1] we have;

`|w-22|\leq 0.12`

Therefore, the specification as an absolute value inequality is ,
`|w-22|\leq 0.12`

Answer 2

For C, we can subtract 0.12 from 21.88 and 22.12 (and make them an absolute value) to get |21.76|≤|w-0.12|≤|22|, which isn't true as 21.76 <22

For B, we can plug it in similarly to get |21.88-22|≤|w-22|≤|22.12-22|=
|-0.12|≤|w-22|≤|0.12|. As making the absolute value of -0.12 into 0.12 would involve multiplying it by something negative, that turns it into
0.12≥|w-22|≤0.12 by switching the sign around. However, this perfectly fits for D, which is therefore correct!