Question

Write an equation in slope-intercept form of a line passingthrough the given point and parallel to the given line.2. (0,4);y=-4/5 x+2

Answer 1

Hello there. To solve this question, we'll have to remember some properties about equations of a line.

We want to write an equation in slope-intercept form of a line, passing through the point (0, 4) and that is parallel to the line y = -4x/5 + 2.

For this, first remember the form of the equation. A equation of a line is in slope-intercept form when it is written as:

`y=mx+b`

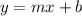
Where m is the slope of the line and b is the y-intercept.

Now, we can figure out the value of b easily, by plugging in the coordinates of the given point.

Plugging x = 0 and y = 4 from the ordered pair (0, 4), we get:

`\begin{gathered} 4=m\cdot0+b \\ 4=b \end{gathered}`

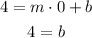
Therefore b = 4.

Now, to find the value for the slope, remember two lines are said to be parallel when their slopes are the same.

We can prove this statement by supposing we have two lines y = m1x + b1 and y = m2x + b2 and knowing parallel lines doesn't intercept in any points of the plane, make sure that they're only parallel when m1 = m2.

Using this fact, we find that the slope of the line has to be the same as the slope of the line:

`y=-(4)/(5)x+2_{}`

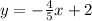
In which we can easily spot the slope: m = -4/5.

Therefore the equation of the line we're looking for is:

`\boxed{y=-(4)/(5)x+4}`

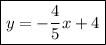
And we can graph both lines as follows: