Question

Which statements are always true regarding the diagram? Check all that apply.

m∠3 + m∠4 = 180°
m∠2 + m∠4 + m∠6 = 180°
m∠2 + m∠4 = m∠5
m∠1 + m∠2 = 90°
m∠4 + m∠6 = m∠2
m∠2 + m∠6 = m∠5

Answer 1

m∠3 + m∠4 = 180° ( RIGHT)
m∠2 + m∠4 + m∠6 = 180° ( RIGHT)
m∠2 + m∠4 = m∠5 ( RIGHT)
m∠1 + m∠2 = 90° (WRONG)
m∠4 + m∠6 = m∠2 (WRONG)
m∠2 + m∠6 = m∠5 (WRONG)

Answer 2

Let's verify each case to determine the solution to the problem.

Statements

case A) m∠3 + m∠4 =
`180\°`

The statement is True

Because

Angle 3 and Angle 4 are supplementary angles

case B) m∠2 + m∠4 + m∠6 =
`180\°`

The statement is True

Because

The sum of the internal angles of a triangle is always equal to
`180\°`

case C) m∠2 + m∠4 = m∠5

The statement is True

Because

we know that

m∠2 + m∠4 + m∠6 =
`180\°` -----> equation A (see case B)

m∠5 + m∠6 =
`180\°` -------> by supplementary angles

m∠6 =
`180\°`-m∠5 -------> equation B

substitute equation B in equation A

m∠2 + m∠4 +
`180\°`-m∠5 =
`180\°`

m∠2 + m∠4 = m∠5 ---------> is ok

case D) m∠1 + m∠2=
`90\°`

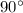
The statement is False

Because

m∠1 + m∠2=
`180\°` -------> by supplementary angles

case E) m∠4 + m∠6=m∠2

The statement is False

Because

we know that

m∠2 + m∠4 + m∠6 =
`180\°`

m∠4 + m∠6 =
`180\°`-m∠2

m∠4 + m∠6=m∠2

`180\°`-m∠2= m∠2

`180\°`=2m∠2

m∠2=
`90\°`

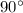
the statement only will be true when the triangle be right triangle and

m∠2=
`90\°`

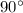
case F) m∠2 + m∠6 = m∠5

The statement is False

Because

we know that

m∠5 + m∠6 =
`180\°` -------> by supplementary angles

m∠5=
`180\°`-m∠6 -----> equation A

m∠2 + m∠6 = m∠5 --------> equation B (given equation)

substitute equation A in equation B

m∠2 + m∠6 =
`180\°`-m∠6

m∠2 + 2m∠6 =
`180\°`

the statement only will be true when the triangle be isosceles and

m∠4=m∠6

therefore

the answer is

m∠3 + m∠4 =
`180\°`

m∠2 + m∠4 + m∠6 =
`180\°`

m∠2 + m∠4 = m∠5