Question

What is the distance between the points (21, -30) and (3, 8)? If necessary, round your answer to two decimal places.

A. 56 units
B. 38 units
C. 33.47 units
D. 42.05 units

Answer 1

The correct option is D.

Explanation:

The distance between two points
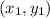`(x_1,y_1)` and
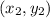`(x_2,y_2)` is defined as

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

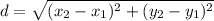
Using distance formula, the distance between two points (21, -30) and (3, 8) is

`d=√((3-21)^2+(8-(-30))^2)`

`d=√((-18)^2+(38)^2)`

`d=√(1768)`

`d=42.0475920833`

`d\approx 42.05`

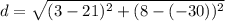
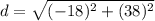
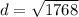
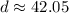
The distance between the points (21, -30) and (3, 8) is 42.05 units. Therefore the correct option is D.

Answer 2

To find the distance, you must know Pythagorean Theorem. Here is how to solve it:

First find the positive distance between the x's: 21-3=18
Then find the positive distance between the y's: 8-(-30)=38
Then use Pythagorean Theorem: (18)^2+(38)^2=(x)^2
After solving you get x is about 42.05 which is D